奇函数加奇函数是什么函数？怎么证明

奇函数四则运算以后该如何判断函数的奇偶性？

hello，大家好，这里是摆渡学涯，很高兴在这跟大家见面了，马上要进入期中考试了，你的复习准备到哪里了？这次课程咱们来讲一下奇函数相关的变形考点，对于奇函数进行四则运算该如何判断函数的奇偶性呢？

1 已知f(x)为奇函数，判断–f(x)的奇偶性

证明：因为f（x）为奇函数，所以f（x）的定义域关于原点对称，且满足：f（x）=-f（-x），因此-f（x）的定义域关于原点对称，且-f（x）=f（-x），令g（x）=-f（x），则g（x）=-g（-x），即g（x）为奇函数，则-f（x）为奇函数。

下面咱们给出个实际的例子：已知f（x）=x，-f（x）=-x，则-f（x）为奇函数。相关的证明你下去自己证明一下吧。（温馨提示，根据奇函数的定义即可证明出来哦。）

2 已知f(x)是奇函数，判断f(-x)的奇偶性

证明：因为f（x）为奇函数，所以f（x）的定义域关于原点对称，且满足：f（x）=-f（-x），因此-f（x）的定义域关于原点对称，且-f（x）=f（-x），令g（x）=-f（x），则g（x）=-g（-x），即g（x）为奇函数，则-f（x）为奇函数。

下面咱们给出个实际的例子：已知f（x）=x，-f（x）=-x，则-f（x）为奇函数。相关的证明你下去自己证明一下吧。（温馨提示，根据奇函数的定义即可证明出来哦。）

3 已知f(x)和g(x)都是奇函数，且定义域相同，判断f(x)g(x)的奇偶性

证明：因为f（x），g（x）为奇函数，所以f（x），g（x）的定义域关于原点对称，且满足：f（x）=-f（-x），g（x）=-g（-x）因此f（x）g（x）的定义域关于原点对称，且f（x）g（x）=f（-x）g（-x），令h（x）=f（x）g（x），则h（x）=h（-x），即g（x）为偶函数，则f（x）g（x）为偶函数。

下面咱们给出个实际的例子：已知f（x）=x，g（x）=-x，则f（x）g（x）=-x的平方为偶函数。相关的证明你下去自己证明一下吧。

4 已知f(x)和g(x)是表达式不互为相反数奇函数，且定义域相同，判断f(x)+g(x)的奇偶性

证明：因为f（x），g（x）为奇函数，所以f（x），g（x）的定义域关于原点对称，且满足：f（x）=-f（-x），g（x）=-g（-x）因此f（x）+g（x）的定义域关于原点对称，且f（x）+g（x）=-f（-x）-g（-x），令h（x）=f（x）+g（x），则h（x）=-h（-x），即g（x）为奇函数，则f（x）+g（x）为奇函数。注意：当两个函数的表达式互为相反数的时候，此时的函数为常数函数，常数函数的奇偶性我们是不做要求的哦。

下面咱们给出个实际的例子：已知f（x）=x，g（x）=2 x，则f（x）+g（x）=-3 x为奇函数。相关的证明你下去自己证明一下吧。

5 已知f(x)和g(x)是不相等的两个奇函数，且定义域相同，判断f(x)-g(x)的奇偶性

根据4相关的证明即可进行相关的证明哦。证明过程留给你自己去证明了。咱们给出结论f（x）-g（x）没有奇偶性（奇偶性不确定）。例如：f（x）=x的三次方，g（x）=x，f（x）-g（x）非奇非偶哦。完整的证明过程你一定要自己去写一下哦，否则你还是不理解奇函数哦。如果你还是没有证明出来，请跟我们一起交流遇到的困难哦。咱们下次课再见吧。当然你也可以考虑一下函数的除法，自己给出证明的。

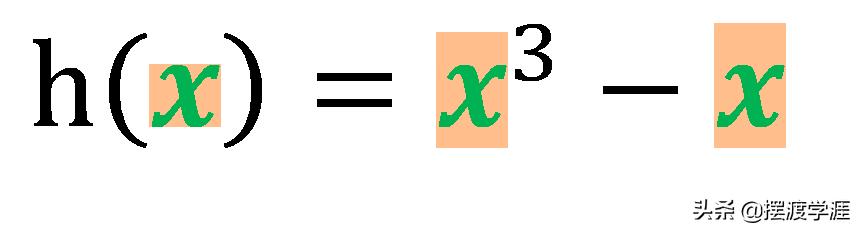
时间关系，本次课程我们就为大家分享到这里了，我们下次课再见。如您有相关的疑问，请在下方留言，我们将第一时间给以大家满意的回复。

声明：本文为摆渡学涯的原创文章，未经作者同意不得进行相关的转载和复制，剽窃者是可耻的。翻版必究。